南京师范大学《高等几何》课程简介 一、课程目标 本课程在学生具备初等几何、解析几何、高等代数、数学分析知识的基础上,系统地学习射影几何的基本知识,使学生能用变换群的观点来看待几何学,加深对几何学的理解,拓展几何空间概念。通过本课程利用商空间思想研究亏格为零不可定向的闭曲面上的几何学的训练,一方面使得学生拓宽眼界,扩大知识领域,提高抽象思维、理性思维能力,为进一步的数学学习打下基础;另一...
高等几何
国家级本课程主要用解析法及综合法研究射影平面上的基本射影图形(如:点列、线束、三点形、三线形、完全四点形、完全四线形、二次曲线等)在射影变换下保持不变的性质和量,射影平面、射影变换本身及性质自然也是讨论重点,Klein变换群几何学观点、平面对偶原则、Desargues透视定理等著名定理更是一些亮点。
南京师范大学《高等几何》课程简介 一、课程目标 本课程在学生具备初等几何、解析几何、高等代数、数学分析知识的基础上,系统地学习射影几何的基本知识,使学生能用变换群的观点来看待几何学,加深对几何学的理解,拓展几何空间概念。通过本课程利用商空间思想研究亏格为零不可定向的闭曲面上的几何学的训练,一方面使得学生拓宽眼界,扩大知识领域,提高抽象思维、理性思维能力,为进一步的数学学习打下基础;另一...
引论
拓广平面
拓广平面上的齐次坐标
射影平面
平面对偶原则
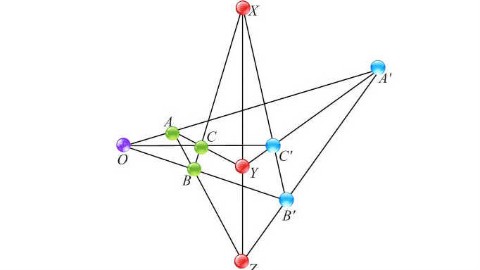
Desargues定理
交比
完全四点形与完全四线形的调和性
一维基本形的射影对应
一维射影变换
一维基本形的对合
二维射影变换
期中考试及期中考试讲评
射影仿射平面
平面上的几个变换群
变换群与几何学
二次曲线的射影定义
Pascal定理和Brianchon定理
配极变换
二次点列上的射影变换
二次曲线的射影分类
二次曲线的仿射理论
二次曲线的仿射分类
期末考试

978-7-03-019657-6
周兴和

978-7-04-008278-4
梅向明 刘增贤 王汇淳 王智秋

978-7-03-043120-2
周兴和,杨明升

978-7-03-038798-1
Xinghe Zhou, Mingsheng Yang
理论课
专业基础课/技术基础课
90.0
南京师范大学
理学
数学类
数学与应用数学
数学与应用数学 信息与计算科学 统计学
31550
6